## Description Catamorphisms are generalizations of the concept of a fold in functional programming. A catamorphism deconstructs a data structure with an F-algebra for its underlying functor. ## History The name catamorphism appears to have been chosen by Lambert Meertens [1]. The category theoretic machinery behind these was resolved by Grant Malcolm [2][3], and they were popularized by Meijer, Fokkinga and Paterson[4][5]. The name comes from the Greek 'κατα-' meaning "downward or according to". A useful mnemonic is to think of a catastrophe destroying something.

Notation
A catamorphism for some F-algebra (X,f) is denoted (|f|)F. When the functor F can be determined unambiguously, it is usually written (|φ|) or cata φ. Due to this choice of notation, a catamorphism is sometimes called a banana and the (|.|) notation is sometimes referred to as banana brackets. ## Haskell Implementation ```haskell type Algebra f a = f a -> a newtype Mu f = InF { outF :: f (Mu f) } cata :: Functor f => Algebra f a -> Mu f -> a cata f = f . fmap (cata f) . outF ``` ## Alternate Definitions ```haskell cata f = hylo f outF cata f = para (f . fmap fst) ``` ## Duality A catamorphism is the categorical dual of an anamorphism. ## Derivation If (μF,inF) is the initial F-algebra for some endofunctor F and (X,φ) is an F-algebra, then there is a unique F-algebra homomorphism from (μF,inF) to (X,φ), which we denote (|φ|)F. That is to say, the following diagram commutes:
## Laws
RuleHaskell
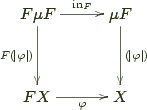
cata-cancel 
cata phi . InF = phi . fmap (cata phi)
cata-refl 
cata InF = id
cata-fusion 
f . phi = phi . fmap f => 
f . cata phi = cata phi
cata-compose 
eps :: forall x. f x -> g x =>
cata phi . cata (In . eps) =
cata (phi . eps)
## Examples The underlying functor for a string of characters and its fixed point. ```haskell data StrF x = Cons Char x | Nil type Str = Mu StrF nil :: Str nil = InF Nil cons :: Char -> Str -> Str cons x xs = InF (Cons x xs) instance Functor StrF where fmap f (Cons a as) = Cons a (f as) fmap f Nil = Nil ``` The length of a string as a catamorphism: ```haskell length :: Str -> Int length = cata phi where phi (Cons a b) = 1 + b phi Nil = 0 ``` The underlying functor for the natural numbers: ```haskell data NatF a = S a | Z deriving (Eq,Show) type Nat = Mu NatF instance Functor NatF where fmap f Z = Z fmap f (S z) = S (f z) ``` Addition as a catamorphism: ```haskell plus :: Nat -> Nat -> Nat plus n = cata phi where phi Z = n phi (S m) = s m Multiplication as a catamorphism: times :: Nat -> Nat -> Nat times n = cata phi where phi Z = z phi (S m) = plus n m z :: Nat z = InF Z s :: Nat -> Nat s = InF . S ``` ## Mendler Style A somewhat less common variation on the theme of a catamorphism is a catamorphism as a recursion scheme a la Mendler, which removes the dependency on the underlying type being an instance of Haskell's Functor typeclass [6]. ```haskell type MendlerAlgebra f c = forall a. (a -> c) -> f a -> c mcata :: MendlerAlgebra f c -> Mu f -> c mcata phi = phi (mcata phi) . outF ``` From that we can derive the original notion of a catamorphism: ```haskell cata :: Functor f => Algebra f c -> Mu f -> c cata phi = mcata (\f -> phi . fmap f) ``` This can be seen to be equivalent to the original definition of cata by expanding the definition of `mcata`. The principal advantage of using Mendler-style is it is independent of the definition of the `Functor` definition for `f`. ## Mendler and the Yoneda Lemma The definition of a Mendler-style algebra above can be seen as the application of the Yoneda lemma to the functor in question. In type theoretic terms, the Yoneda lemma states that there is an isomorphism between `(f a)` and `∃b. (b -> a, f b)`, which can be witnessed by the following definitions. ```haskell data CoYoneda f a = forall b. CoYoneda (b -> a) (f b) toCoYoneda :: f a -> CoYoneda f a toCoYoneda = CoYoneda id fromCoYoneda :: Functor f => CoYoneda f a -> f a fromCoYoneda (CoYoneda f v) = fmap f v ``` Note that in Haskell using an existential requires the use of `data`, so there is an extra bottom that can inhabit this type that prevents this from being a true isomorphism. However, when used in the context of a `(CoYoneda f)`-Algebra, we can rewrite this to use universal quantification because the functor f only occurs in negative position, eliminating the spurious bottom. ```haskell Algebra (CoYoneda f) a = (by definition) CoYoneda f a -> a ~ (by definition) (exists b. (b -> a, f b)) -> a ~ (lifting the existential) forall b. (b -> a, f b) -> a ~ (by currying) forall b. (b -> a) -> f b -> a = (by definition) MendlerAlgebra f a ``` ## Generalized Catamorphisms Most more advanced recursion schemes for folding structures, such as paramorphisms and zygomorphisms can be seen in a common framework as "generalized" catamorphisms[7]. A generalized catamorphism is defined in terms of an F-W-algebra and a distributive law for the comonad W over the functor F which preserves the structure of the comonad W. ```haskell type Dist f w = forall a. f (w a) -> w (f a) type FWAlgebra f w a = f (w a) -> a g_cata :: (Functor f, Comonad w) => Dist f w -> FWAlgebra f w a -> Mu f -> a g_cata k g = extract . c where c = liftW g . k . fmap (duplicate . c) . outF ``` However, a generalized catamorphism can be shown to add no more expressive power to the concept of a catamorphism. That said the separation of a number of the "book keeping" concerns by isolating them in a reusable distributive law can ease the development of F-W-algebras. We can transform an F-W-algebra into an F-algebra by including the comonad in the carrier for the algebra and then extracting after we perform this somewhat more stylized catamorphism: ```haskell lowerAlgebra :: (Functor f, Comonad w) => Dist f w -> FWAlgebra f w a -> Algebra f (w a) lowerAlgebra k phi = liftW phi . k . fmap duplicate g_cata :: (Functor f, Comonad w) => Dist f w -> FWAlgebra f w a -> Mu f -> a g_cata k phi = extract . cata (lowerAlgebra k phi) ``` and we can trivially transform an Algebra into an F-W-Algebra by mapping the counit of the comonad over F. Then using the trivial identity functor, we can represent every catamorphism as a generalized-catamorphism. ```haskell liftAlgebra :: (Functor f, Comonad w) => Algebra f a -> FWAlgebra f w a liftAlgebra phi = phi . fmap extract cata :: Functor f => Algebra f a -> Mu f -> a cata f = g_cata (Identity . fmap runIdentity) (liftAlgebra f) ``` Between these two definitions we can see that a generalized catamorphism does not increase the scope of a catamorphism to encompass any more operations, it simply further stylizes the pattern of recursion. ## References
  1. L. Meertens. First Steps towards the theory of Rose Trees. Draft Report, CWI, Amsterdam, 1987.
  2. G. Malcolm. PhD. Thesis. University of Gronigen, 1990.
  3. G. Malcolm. Data structures and program transformation. Science of Computer Programming, 14:255--279, 1990.
  4. E. Meijer. Calculating Compilers, Ph.D Thesis, Utrecht State University, 1992.
    http://research.microsoft.com/~emeijer/Papers/Thesis.pdf
  5. E. Meijer, M. Fokkinga, R. Paterson, Functional Programming with Bananas, Lenses, Envelopes and Barbed Wire, 5th ACM Conference on Functional Programming Languages and Computer Architecture.
    http://research.microsoft.com/~emeijer/Papers/fpca91.pdf
  6. T. Uustalu, V. Vene. Coding Recursion a la Mendler. Proceedings 2nd Workshop on Generic Programming, WGP'2000, Ponte de Lima, Portugal, 6 July 2000
    http://citeseer.ist.psu.edu/314266.html
  7. T. Uustalu, V. Vene, A. Pardo. Recursion schemes from Comonads. Nordic Journal of Computing. Volume 8 , Issue 3 (Fall 2001). 366--390, 2001 ISSN:1236-6064